Jak serwer sprawdza hasło, skoro nie przechowuje haseł, czyli rzecz o funkcjach skrótu

Dziś zadamy sobie pytanie: w jaki sposób serwis online może sprawdzić poprawność naszego hasła, zarazem nie przechowując owego hasła na serwerze. Kluczowym elementem odpowiedzi będzie tzw. „funkcja skrótu” (funkcja haszująca), która pojawia się w wielu zastosowaniach związanych z kryptografią.

Programiści używają jednak funkcji skrótu także do innych celów. Dowiemy się, dlaczego przy różnych okazjach należy dobierać różne funkcje skrótu i dlaczego niewłaściwy wybór może rodzić poważne konsekwencje.

Starałem się, aby artykuł pozostawał czytelny dla osób spoza branży IT. Nie wiem, czy mi się udało. Jeśli zdarzy się, że zgubisz wątek albo przytłoczy cię liczba nowych słów – po prostu przeskocz do następnego rozdziału.

Na początek kilka pojęć

W poniższym tekście będziemy utożsamiać funkcję skrótu z określonym algorytmem obliczeń przeprowadzanych „w komputerze”. Funkcje skrótu mogą przyjmować dane wejściowe o dowolnej długości. Wynikiem obliczeń będzie tzw. skrót (hasz, ang. hash) czyli ciąg o ustalonej, zawsze takiej samej długości.

Zależnie od specyfiki funkcji skrótu, dane wejściowe będą przetwarzane po jednym bicie (zero lub jedynka), po jednym bajcie (osiem kolejnych bitów) albo w paczkach po kilka bajtów. Jeśli ostatnia paczka nie jest zapełniona, brakujące bajty są dodawane na jeden z kilku ściśle określonych sposobów (tzw. padding).

Skrót obliczany przez wskazaną funkcję jest zawsze tej samej długości. Długość ta podawana jest w bitach lub bajtach (liczba bitów dzielona przez osiem). Często spotykane długości skrótów to 128, 160, 256, 384 lub 512 bitów (odpowiednio 16, 20, 32, 48 lub 64 bajty).

Warto zauważyć, że funkcja skrótu potrafi „obliczyć” także skrót danych o zerowej długości. Prosty przykład zobaczymy już za chwilę.

Najprostsza użyteczna funkcja skrótu

Najprostsza funkcja skrótu będzie zwracała pojedynczy bit danych – czyli wartość zero albo jeden. Co ciekawe, nawet taki najkrótszy możliwy skrót może być przydatny! Tak właśnie działał tzw. bit parzystości, stosowany w latach ‘80 i ‘90 w komunikacji modemowej (komputery komunikowały się wówczas przez analogowe łącza telefonii naziemnej).

Zasada działania bitu parzystości była prosta – do każdego transmitowanego bajtu dołączany był dodatkowy bit informujący, czy liczba jedynek (aktywnych bitów) w owym bajcie była parzysta czy nieparzysta. Jedynka oznacza „tak, liczba była parzysta”, zero oznacza „nie, liczba była nieparzysta”. Dzięki temu możliwe było wykrycie prostych zakłóceń, których w telefonii analogowej nie brakowało. Jeśli jednak przekłamaniu uległy dwa bity (albo cztery, albo sześć itd), kontrola parzystości nie wystarczała do wykrycia takiej sytuacji.

Funkcja obliczająca parzystość jest prosta, do pracy wystarczy jej jedna zmienna (rejestr). Wartość początkowa rejestru parzystości to jedynka. Dla ciągu pustego funkcja zwraca tę właśnie jedynkę, bo zero wczytanych jedynek to parzysta liczba wczytanych jedynek. Dane wejściowe przetwarzane są po jednym bicie. Każde wczytane zero nie wywołuje efektu, każda wczytana jedynka zmienia wartość rejestru parzystości. Gdy funkcja przetworzy komplet bitów wejściowych, jako wynik zwracany jest stan rejestru.

Sumy kontrolne

Tematyce sum kontrolnych poświęciłem jakiś czas temu osobny artykuł, więc zainteresowani mogą skoczyć do niego, przeczytać, po czym wrócić tutaj.

W skrócie – sumy kontrolne to specyficzne funkcje skrótu, których celem jest wykrywanie usterek transmisji danych. Bit parzystości też pasuje do tej definicji, ale będziemy raczej mieć na myśli algorytmy lepiej wykrywające uszkodzenia transmitowanych danych.

Rzadko zdajemy sobie sprawę z tego, że sumy kontrolne pojawiają się niezależnie na wielu różnych warstwach abstrakcji. Oto przykłady:

• gdy pobierasz plik przeglądarką internetową, każdy pakiet TCP/IP niesie ze sobą sumę kontrolną; w przypadku wykrycia niezgodności system operacyjny odbiorcy wyśle nadawcy żądanie retransmisji
• w niezwykle rzadkim przypadku promieniowanie kosmiczne może uszkodzić zawartość pamięci komputera; pamięć RAM typu ECC wykryje (i skoryguje!) przekłamania pojedynczego bitu w każdym bajcie
• jeśli zapiszesz dane na klasycznym dysku twardym, przy próbie odczytu kody CRC pozwolą wykryć (i skorygować!) powstałe usterki
• jeśli zapiszesz dane na macierzy dyskowej typu RAID, kody Reeda-Solomona zapewnią odporność na awarię określonej wcześniej liczby napędów
• jeśli pobrany plik był skompresowany popularnymi algorytmami, jego suma kontrolna jest przechowywana wewnątrz archiwum i zostanie użyta podczas dekompresji (archiwum może też zawierać opcjonalne, nadmiarowe dane korekcyjne)

Jak widać, sumy kontrolne są „w komputerze” wszechobecne, bo i korzyści płynące z ich użycia są oczywiste. O uszkodzeniu danych chcemy wiedzieć jak najszybciej. Jednocześnie jednak nie chcemy poświęcać na tę kontrolę zbyt wiele mocy obliczeniowej, więc…

Szybko i zwięźle

Algorytmy obliczające sumy kontrolne mają być jak najbardziej efektywne. Realizowane przez nie funkcje skrótu będą produkować dość krótkie hasze, z reguły 16- albo 32-bitowe. W niektórych sytuacjach – na przykład wewnątrz potężnych routerów kierujących ruchem o przepustowości dziesiątków terabitów – do sprawdzenia będą sumy kontrolne w miliardach pakietów na sekundę. Takie obliczenia są realizowane przez układy zaprojektowane specjalnie do tego celu.

Gdy jednak wyliczamy sumy kontrolne na „zwykłych” procesorach, pożądaną cechą będzie dodatkowo jak najmniejsze zużycie pamięci. Dzięki temu oprogramowanie działające w oparciu o sieć TCP/IP można uruchamiać nie tylko na mikrokontrolerach, lecz nawet na czterdziestoletnim Commodore 64 z zegarem o częstotliwości 1 MHz.
(kod liczący sumę kontrolną jest tutaj)

Tablice haszujące (mieszające)

Jedną z najczęściej spotykanych w programowaniu struktur danych jest tablica czyli swego rodzaju pudełko z ponumerowanymi przegródkami. Programista określa, jakiego typu dane można przechowywać w pudełku i ile ma być przegródek, a komputer bierze na siebie przypisanie wszystkim numerom przegródek osobnego obszaru pamięci.

Czasem numeracja przegródek będzie oczywista – np. tablica wszystkich numerów telefonicznych w Polsce będzie miała miliard przegródek (tyle mamy kombinacji numerów, od 000 000 000 do 999 999 999). Dane abonenta korzystającego z numeru 12 442 02 44 będzie można znaleźć w przegródce numer sto dwadzieścia cztery miliony, czterysta dwadzieścia tysięcy, dwieście czterdzieści cztery.

Zamiana napisu na liczbę

Jeśli jednak chcielibyśmy uporządkować abonentów według nazwisk, napotkamy problem. Komputer nie umie przypisać przegródkom etykiet tekstowych, nie da się w tablicy oznaczyć przegródki napisem „Jan Kowalski” i potem szybko ją odnaleźć. Nie sposób też wygenerować tylu przegródek, ile jest możliwych nazwisk – pomyślmy tylko o Grzegorzu Brzęczyszczykiewiczu (zam. Chrząszczyszewoszyce, powiat Łękołody).

Z pomocą przyjdą nam funkcje skrótu. Załóżmy, że argumentem będzie napis złożony z imienia, nazwiska i PESEL-u (zależy nam na unikalności napisu). Wartością skrótu będzie jak zwykle liczba z określonego zakresu. Może się zdarzyć, że zakres ten będzie mniejszy, niż liczba osób, dla których będziemy obliczać skróty. Przykład – skrót 24-bitowy może przyjąć jedną z 16.7 miliona wartości, a więc wśród skrótów nazwisk 38 milionów Polaków na pewno znajdziemy duplikaty (mówi o tym tzw. zasada szufladkowa Dirichleta, która zawsze wydawała mi się niepotrzebna, bo to przecież oczywiste).

Okazuje się, że w praktyce nie będzie to problemem. W przegródkach będziemy przechowywać nie dane pojedynczej osoby, lecz listę osób o takim samym skrócie (czyli wskaźniki na właściwe miejsca w pamięci komputera). Nawet, jeśli przy odczycie danych będziemy musieli przejść przez kilkanaście czy kilkadziesiąt pozycji w jednej przegródce, nadal potrwa to bez porównania krócej, niż przejście przez pełną listę kilkudziesięciu milionów rekordów.

Równomierność rozkładu skrótów

W ten sposób dochodzimy do wymogów, jakie będziemy stawiać funkcjom skrótu stosowanym w tego typu tablicach (które w języku programistów są nazywane tablicami asocjacyjnymi, tablicami haszującymi, mapami lub słownikami). Tu szybkość nie będzie już stała na pierwszym miejscu, najważniejszy będzie możliwie równomierny (jednorodny) rozkład skrótów w całym możliwym zakresie wartości.

Przykład: jeśli użyjemy 24-bitowej funkcji skrótu (16.7 miliona przegródek), która weźmie dane 38 milionów Polaków i umieści wszystkich w 19 przegródkach po dwa miliony osób, na pewno nie osiągniemy zakładanych celów. Jeśli funkcja zapełni milion przegródek, a w każdym znajdzie się średnio kilkadziesiąt osób, będzie znacznie lepiej. Im lepsza funkcja, tym więcej przegródek użyje oraz tym rzadsze i mniejsze będą kolizje (spiętrzenia) w jednej przegródce.

W przypadku tablic asocjacyjnych nie będzie nam przeszkadzało podobieństwo skrótów dla podobnych argumentów. Jeśli panowie Kotek i Kołek otrzymają skróty różniące się kilkoma bitami, wszystko jest w porządku. W pewnych sytuacjach może przynieść to nawet pewne korzyści. Przykład: gdy skróty podobnych nazwisk będą liczbami leżącymi blisko siebie, to odczyt pierwszego rekordu przeniesie do pamięci cache procesora także „pobliskie” zestawy – wówczas odwołanie do nich będzie szybsze, niż przy dostępie losowym.

Na podobnej zasadzie działa filtr Blooma – algorytm bardzo szybkiego, lecz niedokładnego wyszukiwania danych. Przyda się wszędzie tam, gdzie i tak zastosowane będą zaokrąglenia – np. w artykule opisującym aktywność zawodową społeczeństwa, gdzie liczby opisujące formy zatrudnienia podane zostaną z dokładnością do tysięcy lub dziesiątek tysięcy.

Przykłady funkcji skrótu

Zanim pójdziemy dalej, popatrzymy sobie na kilka funkcji skrótu, określonych w bardzo różny sposób. Na pierwszy ogień pójdzie…

Skrót obrazka

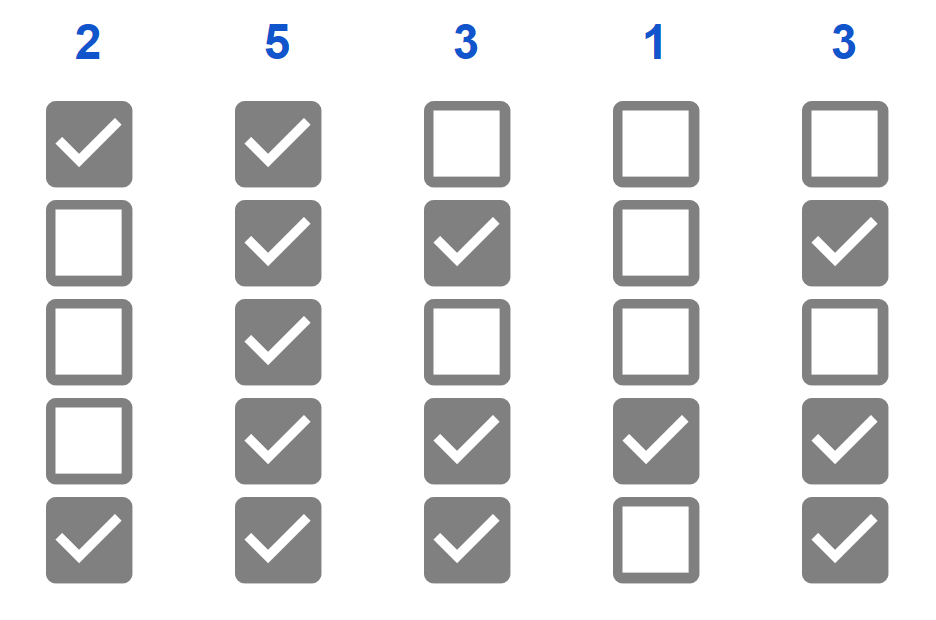
Weźmy siatkę 5×5 pikseli, z których każdy może być zapalony lub zgaszony. Liczba możliwych kombinacji to 2²⁵ czyli ponad 33 miliony.

Skrót wygenerujemy następująco: zliczymy zapalone bity w każdej kolumnie pikseli z osobna i tak wyznaczone cyfry połączymy w napis stanowiący skrót. Możliwych skrótów będzie 6⁵ czyli dokładnie 7776 (każda cyfra skrótu przyjmuje wartość od 0 do 5, to sześć wartości). Skrót powyższego obrazka to 25313.

Spostrzeżenia:

• choć skróty 00000 i 55555 jednoznacznie określają układ pikseli, to już skrót 00001 odpowiada pięciu możliwym układom.
• każda z pięciu cyfr skrótu niesie informacje o osobnym fragmencie obrazu, fragmenty nie wpływają na siebie
• niewielkie zmiany obrazka skutkują niewielkimi zmianami lub brakiem zmiany skrótu

Użyteczność: pokazana funkcja nie ma sensownego zastosowania – celem przykładu było pokazanie, że do wyliczenia tego prostego skrótu wystarczy umiejętność dodawania na palcach jednej ręki

Funkcja XOR

XOR (eXclusive OR) to funkcja binarna, której argumentem są dwa bity a wartością – bit wynikowy ustawiony na 1 wtedy, gdy wśród bitów wejściowych dokładnie jeden był zapalony. Innymi słowy:

Algorytm obliczania skrótu będzie działać następująco:

WYNIK = 0
dopóki dostępny kolejny bajt:
    do zmiennej ABC wczytaj kolejny bajt
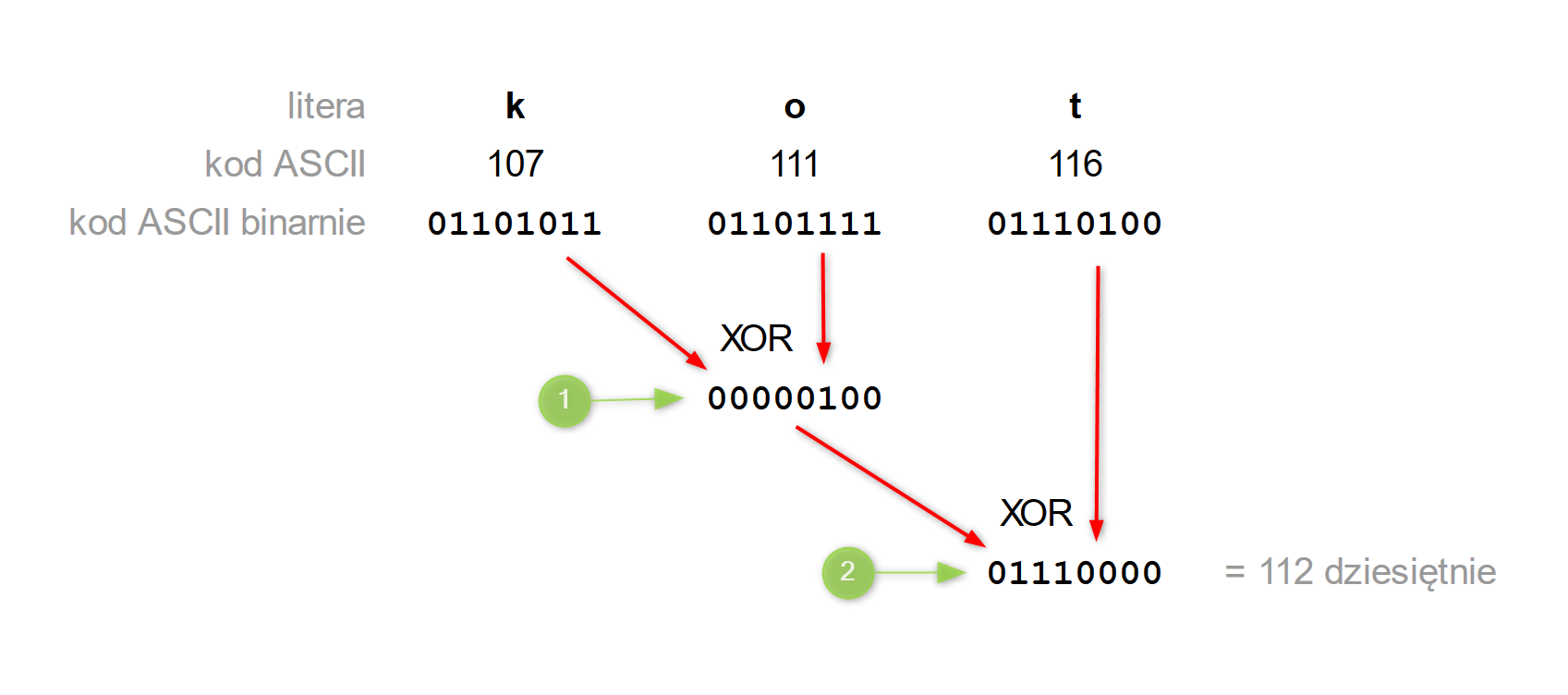
    do zmiennej WYNIK zapisz wynik operacji bitowej ABC XOR WYNIK

Przykład: obliczenie skrótu słowa „kot”.

W pierwszym kroku obliczamy wartość XOR dla liter „k” i „o”, w drugim kroku wartość XOR dla wyniku kroku pierwszego i litery „t”. Wynikiem jest liczba 112.

Spostrzeżenie: zamiast bloków po 8 bitów, jak powyżej, możemy operować na blokach o innej długości, aby otrzymać pożądaną liczbę możliwych wartości skrótu („przegródek”).

Użyteczność: choć sposób liczenia sumy kontrolnej przy użyciu operacji XOR ma wiele wad, np. w porównaniu do funkcji z rodziny CRC, to dzięki swojej prostocie znalazł zastosowanie m.in. w protokole NMEA stosowanym w odbiornikach GPS

Algorytm djb2

unsigned long WYNIK = 5381
dopóki dostępny kolejny bajt:
    do zmiennej BAJT wczytaj kolejny bajt
    do zmiennej WYNIK zapisz wynik operacji: WYNIK * 33 + BAJT

Tym razem zmienna wynik będzie typu unsigned long, czyli 32-bitowa wartość bez znaku. Wartość początkowa „5381” oraz mnożnik „33” zostały wyznaczone przez autora algorytmu w taki sposób, aby zminimalizować liczbę kolizji. Funkcja pozostaje przy tym skrajnie szybka, tutaj można zapoznać się z eksperymentalnymi pomiarami prędkości i liczby kolizji napotykanych w tej i kilku innych prostych funkcjach.

Spostrzeżenie: zamiast wartości 33 można użyć liczby 261, która nieco szybciej „przepycha” początkowe wartości w stronę najbardziej znaczących bitów (opinia autora funkcji)

Użyteczność: funkcja djb2 nadaje się do użycia tam, gdzie potrzebny jest skrót 32-bitowy – np. przy konstruowaniu tablic asocjacyjnych

Cyfry kontrolne

Z sumami kontrolnymi mamy do czynienia w codziennym życiu – jest to cyfra kontrolna (jedna lub dwie) w numerach PESEL, NIP, REGON, IBAN, w numerach dowodów osobistych, paszportów i nie tylko. Zestaw artykułów na ten temat, wraz z algorytmami weryfikacji i przykładowymi obliczeniami, można znaleźć na stronie romek.info

Użyteczność: cyfry kontrolne zapobiegają znakomitej większości literówek przy przepisywaniu numerów PESEL, NIP itd.

Skróty kryptograficzne

Pomału zbliżamy się do pytania tytułowego – jak serwer sprawdza hasło, skoro nie przechowuje haseł? Chcemy osiągnąć stan, w którym wykradziona baza danych użytkowników naszego systemu nie da atakującemu żadnych istotnych informacji, w szczególności nie pozwoli na poznanie haseł.

Otóż – trzecim istotnym obszarem zastosowań funkcji skrótu jest kryptografia. Zamiast zapisywać w bazie danych hasło, zapiszemy jego skrót, dzięki czemu złodziej bazy danych nie pozna oryginalnego hasła, dziękujemy, pozamiatane.

Aha, nie tak szybko. Sam pomysł jest dobry, ale żadna z poznanych wyżej funkcji skrótu nie nadaje się do tego celu. Zastanówmy się, jakie kryteria musi spełniać funkcja-kandydatka.

Kolizja prowadząca do wybranego skrótu

Pierwszy, najbardziej podstawowy problem – gdy atakujący patrzy na ukradziony skrót, nie może dysponować metodą na znalezienie hasła prowadzącego do tego skrótu. Spójrzmy na przykład z haszem obrazka – wystarczy jedno spojrzenie na pięć cyfr skrótu, by od razu przygotować pasującą kombinację kratek-bitów. Nie ma znaczenia, czy jest ona identyczna z pierwowzorem. Ważne, że zgadza się hash. Z tego samego powodu do zastosowań kryptograficznych nie przydadzą się funkcje XOR ani CRC, w przypadku których równie prosto wygenerować jawny tekst prowadzący do poszukiwanego skrótu.

W kryptografii to zagadnienie bezpieczeństwa – tzw. preimage resistance – jest dzielone na dwie kategorie. Pierwsza to odnajdywanie tekstu generującego wybrany skrót, druga to odnajdywanie kolizji czyli tekstu generującego taki sam skrót, jak inny znany tekst. Z naszego punktu widzenia nie ma to większego znaczenia. Chodzi po prostu o to, aby takie odnajdywanie jawnego tekstu było całkowicie niemożliwe.

Od strony filozoficznej ten kawałek chwieje się najbardziej. Dla żadnej z nowoczesnych funkcji skrótu nie dysponujemy matematycznym dowodem, że nie da się jej „odwrócić”. Nie da się dowieść, że jedynym sposobem odzyskania haszowanych haseł jest wypróbowanie wszystkich możliwych kombinacji danych wejściowych (jest to tak zwany atak siłowy, ang. brute-force). Zaufanie pokładane w stosowanych powszechnie funkcjach opiera się jedynie na tym, że nikomu nie udało się odnaleźć takiego sposobu.

Pełna losowość i niezależność każdego bitu

Aby było jasne – każda z rozpatrywanych tu funkcji jest w pełni deterministyczna czyli dla takich samych danych wejściowych zwróci zawsze jednakowy wynik. Oczekujemy jednak, że:

• każdy bit skrótu przyjmie wartość 0 lub 1 z prawdopodobieństwem 50%
• przy zmianie jednego bitu w danych wejściowych, każdy bit skrótu będzie miał 50% szans na zmianę wartości

Przy konstruowaniu tablic asocjacyjnych, podobieństwo skrótów wyliczonych dla podobnych danych wejściowych mogło być pożądane. W zastosowaniach kryptograficznych jest to wykluczone. Nawet jednobitowe różnice pierwotnego tekstu muszą generować skróty w których nie da się znaleźć żadnych związków ani regularności (uwaga na uproszczenie – to bardziej praktyczna obserwacja niż ścisły wymóg matematyczny).

Możliwość ograniczenia długości ciągu wejściowego

Funkcje haszujące ogólnego przeznaczenia muszą akceptować ciąg wejściowy o dowolnym rozmiarze, bo bywają używane do wyliczania skrótu plików o nie dającej się przewidzieć wielkości. W przypadku funkcji generujących skrót na podstawie hasła możemy osłabić ten wymóg – np. niektóre implementacje funkcji bcrypt haszują tylko pierwsze 72 bajty danych wejściowych. Taki rozmiar z reguły pomieści hasło oraz… sól i pieprz (o tych przyprawach napiszemy za chwilę).

Niska (!) wydajność

Ten wymóg jest dość paradoksalny – w końcu rozwój cyfrowych technik obliczeniowych od zawsze miał na celu podnoszenie wydajności obliczeń. Przez kilkadziesiąt lat aktualność zachowywało tzw. prawo Moore’a czyli obserwacja, że gęstość upakowania tranzystorów w układach scalonych podwajała się co 18-24 miesiące. Równolegle doskonalono także algorytmy, by jak najefektywniej wykorzystać nowe funkcje procesorów.

Możemy eksperymentalnie wyznaczyć liczbę cykli, których algorytm obliczający funkcję skrótu potrzebuje do przetworzenia kolejnego bajtu danych wejściowych. W zależności od algorytmu i architektury procesora, będzie to od kilku do kilkudziesięciu instrukcji (przykładowe statystyki tutaj i tutaj). Jak szybko rosła wydajność systemów komputerowych? Oszacujemy to jedynie z grubsza.

Po pierwsze – częstotliwość taktowania zegarów wzrosła z megaherców do gigaherców, to tysiąckrotny wzrost wydajności. Po drugie – instrukcje wektorowe i przetwarzanie wielopotokowe zwiększyły kilkunastokrotnie „uzysk” z jednego cyklu zegarowego. Po trzecie – do gry weszły karty graficzne, których sercem jest zamknięty w jednym chipie zestaw nawet kilkunastu tysięcy niezależnych jednostek obliczeniowych. Można przyjąć, że w ciągu minionych 40 lat moc obliczeniowa dostępna dla typowego Kowalskiego wzrosła sto milionów razy.

W roku 2019 metodą siłową złamano skróty maksymalnie ośmioznakowych haseł znalezionych w kopii unixowego systemu BSD 3 z lat ‘70 ubiegłego wieku – w tym hasło Kena Thompsona (p/q2-q4!), Dennisa Ritchiego (dmac) czy Erica Schmidta (wendy!!!).

Co zrobić, aby nasze hasła nie poddały się hobbystom żyjącym w roku 2070? Okazuje się, że dziś mamy ku temu odpowiednie narzędzia, działające na kilka różnych sposobów. Już przy projektowaniu systemu zabezpieczeń zadbamy o to, aby złodziejom bazy danych jak najbardziej uprzykrzyć życie.

Jak utrudnić łamanie wykradzionych skrótów?

Wiemy już, że serwer nie zapisuje naszego hasła, lecz jego skrót. Wiemy też, że skrót wyliczony przez porządną funkcję haszującą nie zdradzi żadnych informacji o naszym haśle, zaś jedyną metodą odgadnięcia hasła będzie podstawianie różnych możliwych haseł do tej samej funkcji i sprawdzanie zgodności wyliczonego skrótu.

Oczywiście złodzieje wypróbują najpierw te hasła, które już kiedyś wyciekły, np. „12345678”, „qwerty123” albo „1q2w3e4r”. Mogą wręcz zawczasu obliczyć ich skróty i sprawdzić, które powtórzą się wśród skrótów wykradzionych (rozszerzeniem takiej metody będą tęczowe tablice, ang. rainbow tables). Natychmiast będzie też widać, którzy użytkownicy korzystają z takiego samego hasła – skróty ich haseł będą identyczne. Obu problemom zapobiegnie…

Solenie haseł

Wielu użytkowników korzysta z haseł składających się ze słowa lub słów obecnych w słownikach, więc ich złamanie siłowe jest kwestią kilku chwil. Receptą jest wzmocnienie haszy poprzez dodanie do haseł kilkudziesięciu losowych znaków, innych dla każdego użytkownika. Dodatek taki nazywany jest solą (ang. salt) a cały proces – „soleniem” haseł. Sól przechowywana jest w bazie danych obok skrótu.

Widać od razu, że użytkownicy z identycznymi hasłami lecz odmiennymi wartościami soli otrzymają różne wartości skrótu. Bezużyteczne stają się też tablice obliczonych uprzednio skrótów, bo teraz żadna z haszowanych wartości „sól+hasło” nie występuje w jakimkolwiek słowniku.

Niektóre algorytmy kryptograficzne wymuszają przekazanie soli jako parametru, co do pewnego stopnia zabezpiecza system przed błędami wynikającymi z niekompetencji programisty (np. zwolni go z decyzji, czy podczas haszowania sól powinna być dołączona przed czy po pierwotnym haśle).

Sól i… pieprz

Niekiedy w użyciu jest jeszcze jeden dodatek – nazywany pieprzem (ang. pepper). Będzie wspólny dla wszystkich użytkowników, lecz jego wartość będzie składowana poza bazą danych (może być to plik, zmienna środowiskowa, repozytorium sekretów itd). Pieprz pomoże więc w sytuacji, gdy włamywacz uzyskał dostęp jedynie do bazy danych. Zamiast sytuacji „znana sól + być może proste hasło” złodziej będzie się musiał zmierzyć z sytuacją „znana sól + nieznany pieprz + być może proste hasło” – a pieprz może być długi i losowy. Wówczas szanse na odtworzenie choć jednego hasła dramatycznie maleją.

Funkcja skrótu wygrywająca z postępem technicznym

Jak zagwarantować, że siłowe łamanie naszych haseł – dziś niemożliwe – pozostanie niemożliwe także za 50 i 100 lat? Cóż – gwarancji nie mamy żadnej, funkcje skrótu uznawane dziś za bezpieczne mogą zawierać nieznane jeszcze słabości. Na razie jednak wygrywamy z postępem technicznym (lub nakładami finansowymi atakujących) jedną prostą sztuczką.

Iteracje haszowania to wyliczanie skrótu z… już wyliczonego skrótu. Dobra, troszkę tu upraszczam, ale chodzi mniej-więcej właśnie o to. Jeśli obliczenie skrótu zajmuje milionową część sekundy, to w ciągu sekundy złodziej wypróbuje milion potencjalnych haseł. Gdy pierwotne hasło przehaszujemy iteracyjnie sto tysięcy razy, to w ciągu sekundy złodziej będzie w stanie wypróbować jedynie dziesięć potencjalnych kombinacji.

Liczba iteracji jest parametrem występującym w wielu współczesnych funkcjach skrótu (zazwyczaj jako wykładnik, np. „12” oznacza 2¹² iteracji) i jest dopisywana do wyliczonego skrótu. W ten sposób w bazie danych mogą koegzystować skróty o różnej liczbie iteracji, aby – w razie podnoszenia poziomu zabezpieczeń – system mógł przy najbliższym logowaniu podmienić bieżący skrót na bezpieczniejszy.

Notka techniczna – w większości algorytmów nie da się „dohaszować” znanego skrótu bez znajomości hasła, bo w kolejnych przebiegach algorytmu używane są wartości rejestrów roboczych.

Funkcja skrótu wygrywająca z GPU

Pamiętamy, że chipset karty graficznej zbudowany jest z tysięcy niezależnych jednostek obliczeniowych. Wszystkie one mają jednak pewną słabość – dysponują niewielką ilością szybkiej pamięci podręcznej. Jeśli funkcja skrótu będzie wymagała alokacji nie kilkuset bajtów, lecz wielu megabajtów, wydajność obliczeń gwałtownie spadnie – nawet do poziomu kilkurdzeniowego procesora.

Funkcje skrótu takie, jak Argon2, przyjmują pożądane zużycie pamięci jako parametr wejściowy. Oznacza to, że niezależnie od postępów w konstrukcji GPU, w przyszłości nadal możliwe będzie użycie wartości wykraczającej poza możliwości przyszłych generacji sprzętu.

Funkcja skrótu wygrywająca z ASIC

ASIC to specjalizowany układ scalony realizujący tylko jeden rodzaj obliczeń, za to diablo szybko. Przykład: koparki bitcoina Antminer są projektowane do liczenia skrótów SHA256 z maksymalną możliwą wydajnością (moją gawędę o kryptowalutach znajdziesz tutaj). Różnice faktycznie porażają. Antminer liczy setki tysięcy miliardów haszy na sekundę – to kilkadziesiąt tysięcy razy szybciej, niż karta graficzna, i kilkaset tysięcy razy szybciej, niż najnowocześniejsze procesory.

Czy da się obronić przed taką siłą? Tak, jeśli zaprojektujemy algorytm haszujący w sposób dający odporność na jego sprzętowe implementacje „w krzemie”. Dobrym przykładem była funkcja Ethash używana do niedawna w kryptowalucie Ethereum. Po pierwsze wymuszała korzystanie z dużej ilości pamięci RAM, po drugie algorytm obliczeń podlegał cyklicznym zmianom. Gdyby nawet na rynku pojawił się odpowiedni ASIC, nie zdążyłby na siebie zarobić – twórcy Ethereum zareagowaliby kolejną modyfikacją funkcji skrótu.

Jak skonstruowane są prawdziwe funkcje skrótu?

Zrozumienie mechanizmu mieszającego w funkcji skrótu jest dość proste – wystarczy rozumieć podstawowe operacje na bitach (OR, XOR, AND, NOT) i słowach (sumowanie, rotacja bitów).

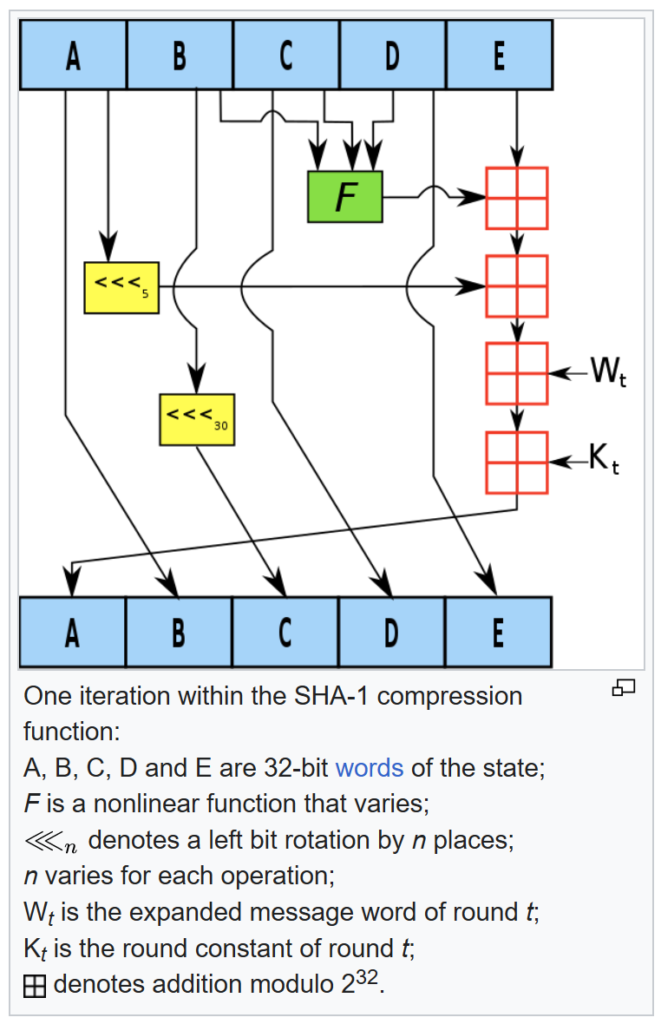
Spójrzmy na pojedynczą operację zmieniającą stan w algorytmie SHA-1, w pojedynczym przebiegu funkcji taka operacja jest powtarzana 80 razy. Funkcja oznaczona na zielono ma cztery warianty podmieniane podczas obliczeń, zainteresowani znajdą rozpiskę w Wikipedii.

Na blogu Gary’ego Fredericksa można znaleźć wizualizację obliczeń prowadzących do wyliczenia wartości SHA-1 dla napisu „denny” – wraz z pośrednimi wartościami rejestrów. Obrazek zapisany jako PNG ma 1024×41472 pikseli, alternatywą dla niego jest poniższa animacja.

O ile zrozumienie schematu mieszania jest proste, o tyle dogłębne poznanie stojącej za nim złożoności wymaga wieloletnich studiów. Wielokrotnie okazywało się bowiem, że algorytmy uznawane za bezpieczne mają pewne słabości.

Co poszło nie tak w starszych algorytmach?

W przypadku (matematycznie) doskonałej funkcji skrótu – o ile takie w ogóle istnieją – ze skrótami o długości n bitów, znalezienie kolizji może wymagać wypróbowania 2ⁿ+1 różnych argumentów (pamiętamy zasadę szufladkową Dirichleta). Oczekiwana liczba kombinacji jest dużo mniejsza i ma związek z paradoksem urodzin, ale ten temat pomijamy.

Wyobraźmy sobie teraz, że w wynikach działania naszej funkcji skrótu spostrzegamy następującą regularność – bity nr 6, 7 i 8 wygenerowanego skrótu są sobie równe. Jeśli potrafimy dowieść, że tak będzie zawsze, udowodnimy tym samym, że liczba możliwych skrótów jest czterokrotnie mniejsza, niż sądziliśmy uprzednio. Będzie ich więc 2^n-2. Wiemy, że atak siłowy powiedzie się na pewno w 1/4 wcześniej zakładanego czasu.

Jeszcze większym odkryciem byłoby odnalezienie zależności między danymi wejściowymi a skrótem, czyli sterowania pewnymi bitami skrótu. Wówczas otworzy się możliwość generowania kolizji – wystarczy znaleźć parę podobnych skrótów i wykorzystać odnalezioną zależność.

Słabości funkcji skrótu są z reguły odkrywane stopniowo, na przestrzeni wielu lat. W przypadku opisywanej wyżej funkcji SHA-1, pierwsze częściowe sukcesy naukowcy ogłosili w roku 2005. Jedna z prac z roku 2010 sugerowała, że koszt wymagany do wygenerowania kolizji SHA-1 przekraczałby 2.5 miliona dolarów. Pierwszą prawdziwą kolizję – dwa różne pliki PDF o tym samym skrócie SHA-1 – opublikowano w roku 2017. Według współczesnych szacunków, moc obliczeniową potrzebną do wyliczenia kolizji można kupić od dostawców chmurowych za kilkanaście/kilkadziesiąt tysięcy dolarów.

Znacznie gorzej upływ czasu zniosła popularna niegdyś funkcja MD5 i jej poprzedniczki, MD2 czy MD4. Usterki ich konstrukcji okazały się poważniejsze – wyliczenie kolizji trwa na zwykłym pececie mniej, niż sekundę a w zaledwie kilka godzin można wygenerować dla MD5 kolizję w wybranym obszarze pliku (np. w nieużywanym bloku komentarza). Więcej o kolizjach przeczytacie w notatkach Ange Albertiniego.

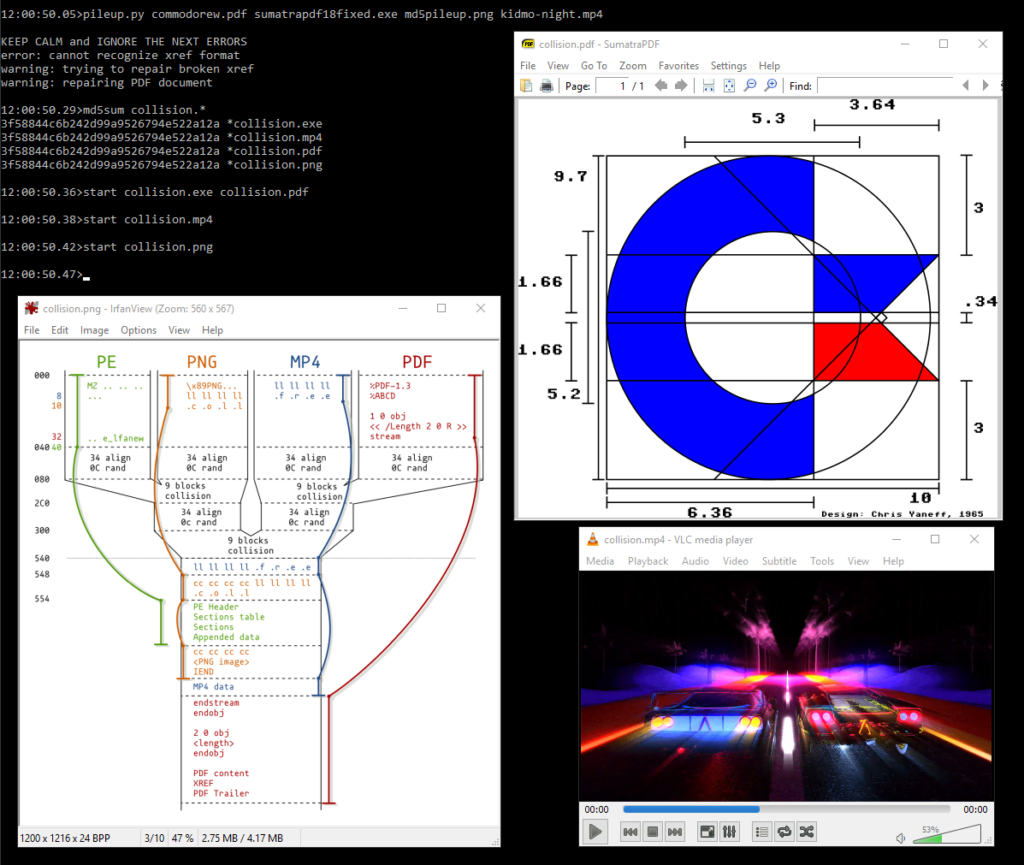
Ważna informacja – do dziś nie odnaleziono w funkcjach MD5 i SHA-1 sposobu na odnajdywanie takich danych, by w wyniku ich haszowania uzyskać wybrany uprzednio skrót.

Co z tego, że ktoś wielkim kosztem obliczy jedną kolizję?

Nasze rozważania rozpoczęliśmy od tematu bezpiecznego uwierzytelniania i wykradania bazy danych ze skrótami haseł. Czy powinniśmy przejmować się opisywanymi słabościami, skoro solony i pieprzony skrót SHA-1 także dziś oprze się atakowi siłowemu? A nawet, jeśli się nie oprze, to co z tego? Atakujący wydadzą fortunę na złamanie raptem jednego z milionów wykradzionych skrótów.

Cóż, kryptolodzy nie bawią się w takie rozważania. Wystarczy jedno nieznaczne naruszenie oczekiwanego poziomu bezpieczeństwa algorytmu, aby rozpoczęło się poszukiwanie alternatyw. A ponieważ braku słabości udowodnić nie sposób, międzynarodowe środowisko kryptologów stale pracuje nad odkrywaniem słabości w tych funkcjach skrótu, które kiedyś zastąpią SHA-2 i SHA-3, uznawane dziś za bezpieczne.

Pamiętajmy, że haszowanie haseł to nie jedyne zastosowanie funkcji skrótu. Są one używane także w podpisach cyfrowych – tam wystarczyłaby pojedyncza kolizja, aby złośliwy malware skutecznie podszył się pod inny, zaufany program.

O czym nie wspomnieliśmy?

Niniejszy artykuł nie wyczerpał wszystkich zagadnień związanych z funkcjami skrótu. Zainteresowany czytelnik może poszukać odpowiedzi na następujące pytania:

• dlaczego kiedyś do Facebooka dało się zalogować mimo podania hasła z Caps-Lockiem? Czy oznacza to, że Facebook zapisywał hasło gołym tekstem?
• jak to możliwe, że bank pyta nas o hasło maskowane (tylko niektóre znaki hasła, za każdym razem inne), skoro te wybrane znaki nie wystarczą do obliczenia pełnego skrótu?
• czy obliczanie skrótu po stronie klienta i wysyłanie go do serwera obniża czy podnosi bezpieczeństwo systemu?

Nie wspomnieliśmy o związkach funkcji skrótu z podpisami cyfrowymi ani o tym, jak różne metody paddingu mogą wpływać na bezpieczeństwo skrótów kryptograficznych.

Świadomie pominęliśmy cały (ogromny!) aparat matematyczny używany w kryptografii. Jeśli chcesz na serio zająć się tematem, nie obejdzie się bez algebry i kombinatoryki na poziomie akademickim.

Celem artykułu było objaśnienie problemów prostym językiem, więc znalazły się w nim liczne uproszczenia.

Podsumowanie

Kluczowa informacja z niniejszego tekstu: kryptograficzna funkcja skrótu (funkcja haszująca) przekształca dowolny zestaw bajtów w skrót (hasz, hash) o ustalonej długości. Jeśli użyliśmy nowoczesnej funkcji, to nie ma żadnego sposobu, aby patrząc na skrót dowiedzieć się czegokolwiek o danych wejściowych, ani by odtworzyć ciąg bajtów generujących taki sam skrót w sposób inny, niż metodą siłową (czyli sprawdzania wszystkich możliwych kombinacji).

Funkcje dawniej uznawane za bezpieczne (MD5, SHA-1) okazały się podatne na odnajdywanie lub wręcz konstruowanie kolizji – różnych danych wejściowych prowadzących do takiego samego skrótu. W funkcjach takich, jak SHA-2 albo SHA-3, nie odnaleziono na razie istotnych usterek.

---

Za uwagi do roboczej wersji tekstu dziękuję Borysowi i Redfordowi