Śnieżka, Kasprowy i Wyspy Tonga

W sobotę 15 stycznia 2022 na południowym Pacyfiku miała miejsce potężna erupcja wulkanu Hunga Tonga. Fala uderzeniowa miała tak dużą siłę, że nawet w Polsce odnotowano skok ciśnienia atmosferycznego. W jednej ze stacji telewizyjnych trafiłem na wypowiedź eksperta, który zastanawiał się, czemu stacje meteo na Śnieżce i Kasprowym Wierchu zarejestrowały to zdarzenie niemal w tej samej chwili. Wydało mu się to trudne do wytłumaczenia z powodu dużej odległości dzielącej te obserwatoria.

Ja z kolei zdziwiłem się, że ekspert się zdziwił, ale potem nabrałem wątpliwości, czy moja intuicja była zgodna rzeczywistością. W niniejszej blogonotce pokazuję, jak szybko i prosto przygotować w języku R ilustracje i obliczenia pozwalające sprawdzić, skąd i z jaką prędkością dobiegło do nas odległe echo wybuchu.

Najpierw zbierzmy dane z Wikipedii. Współrzędne wulkanicznej wyspy Hunga Tonga to 20.536°S 175.382°W (ułamki dziesiętnie). Kasprowy Wierch – 49.231°N, 19.981°E. Śnieżka – 50.735°N, 15.739°E. Teraz wprowadźmy te dane do skryptu języka R. Do wyliczania odległości użyjemy funkcji distVincentyEllipsoid z biblioteki geosphere. Choć Ziemia jest geoidą, to jej kształt dobrze przybliża elipsoida – gdy użyjemy współrzędnych z trzema miejscami dziesiętnymi, nasze obliczenia korzystające z układu odniesienia WGS 84 będą miały dokładność około 0.1 km.

Wypróbujmy tę funkcję na Śnieżce i Kasprowym:

Wyliczona odległość to 347.1 km. Szybka weryfikacja – Google Earth podaje…

… praktycznie tę samą wartość. Metoda działa.

Policzmy wobec tego odległości obu szczytów do wulkanu Hunga-Tonga-Hunga-Ha’apai (jego współrzędne są ujemne, bo Tonga leży na półkuli zachodniej / południowej)

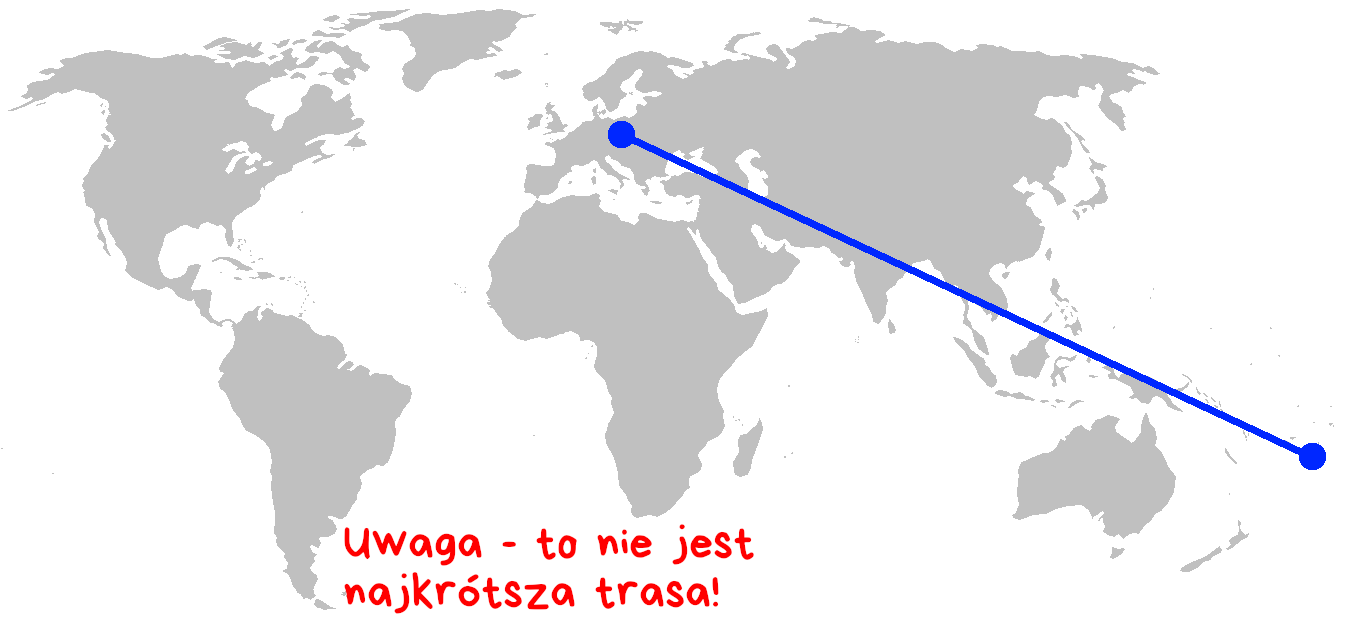
Odległości te różnią się o… niecałe 28 kilometrów? Jak to możliwe? Otóż – najkrótsza trasa łącząca Polskę i Wyspy Tonga nie wygląda tak, jak na obrazku poniżej.

Do takiej mapy świata przyzwyczaiła nas szkoła, ale wyznaczanie trasy na mapie „od linijki” sprawdza się tylko przy mapach dużej skali, pokazujących niewielki obszar. Wiemy, że coś nie gra. Gdyby fala uderzeniowa faktycznie dobiegła do Polski od strony Morza Czarnego / Indii / Indonezji – spodziewalibyśmy się sporego opóźnienia między Kasprowym Wierchem a Śnieżką.

Tymczasem na Kasprowym była to 20:23 czasu lokalnego:

🔎Ciekawostka:
Fala uderzeniowa (ciśnienie powietrza), powstała po wybuchu wulkanu na wyspie Tonga na Pacyfiku, dotarła na Kasprowy Wierch 0 godzinie 20:23 czasu lokalnego. 🧐Widać to na wykresie ciśnienia.
Erupcja miała miejsce około 06:00 rano. ➡️#Tongaeruption pic.twitter.com/cLxepGLXsf

— IMGW-PIB METEO POLSKA (@IMGWmeteo) January 15, 2022

a na Śnieżce… też około 20:20 (uwaga, na obrazku skala czasu w UTC)

Jak już informowaliśmy, po erupcji wulkanu na Pacyfiku w okolicy wysp Tonga barometry na stacjach meteo #IMGW zanotowały skoki i spadki ciśnienia o ok. g. 19:30 UTC, ale również później o około g. 01:30 UTC (fala wtórna). Poniżej dane ze stacji #Śnieżka i #Kielce.
#Tongaeruption pic.twitter.com/KziV0Ri4kJ

— IMGW-PIB METEO POLSKA (@IMGWmeteo) January 16, 2022

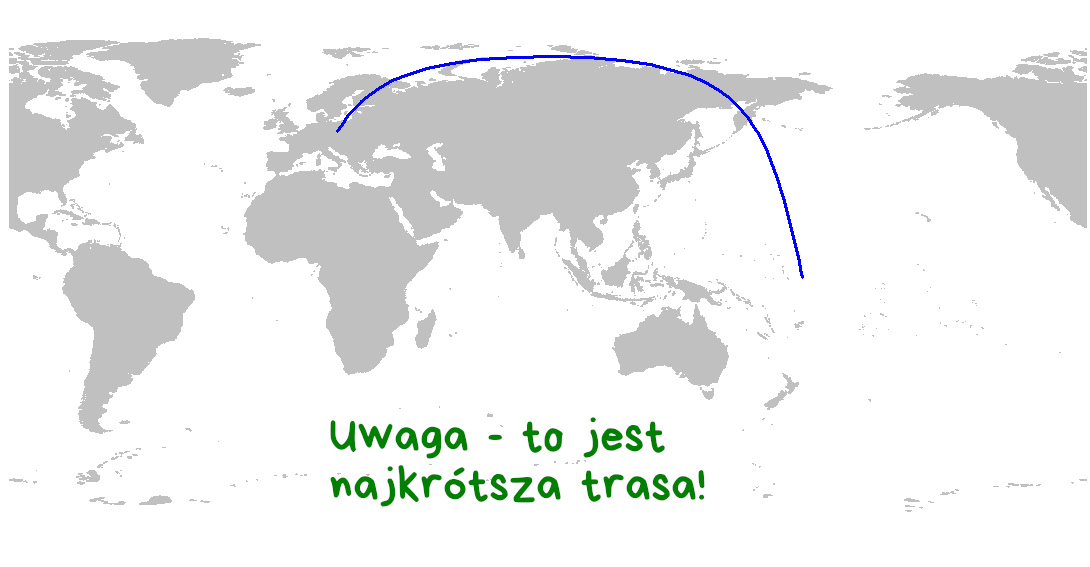
Rozwiążmy tę zagadkę. Gdy odległości rosną na tyle, by znaczenie miała krzywizna Ziemi, musimy wyliczać ortodromę stanowiącą najkrótszą trasę między dwoma punktami. I tu niespodzianka – grzmot doleciał do nas od… północnego wschodu, wcześniej mijając Finlandię, Nową Ziemię i Kamczatkę! Narysujmy to sobie w R, przy użyciu biblioteki maps.

Ponownie do weryfikacji wykorzystamy Google Earth – tu nie ma już wątpliwości, że patrzymy na wycinek koła wielkiego.

Jak szybko przemieszczała się fala uderzeniowa?

Erupcja miała miejsce o godzinie 4:14:45 UTC. Na Kasprowym skok ciśnienia odnotowano o 19:23 UTC. Odstęp czasowy to

> period_to_seconds( lubridate::hm("19:23") - lubridate::hm("4:14") ) / 60
[1] 909

… 909 minut, podczas których fala uderzeniowa pokonała 16543 km, co daje średnią prędkość 1092 km/h.

Możemy stąd wyliczyć, że na Śnieżce pomiar musiał mieć miejsce…

24 km / 1092 km/h = 1.3 min

… niecałe półtorej minuty wcześniej (pamiętacie WolframAlpha? do takich obliczeń jest najlepszy!) Teraz rozumiemy już zdziwienie eksperta z telewizji – gdyby dźwięk doleciał od strony Morza Czarnego, różnica czasu, tym razem na korzyść Kasprowego, wynosiłaby 19 minut.

Podsumowanie

Odbiegliśmy dziś nieco od głównej tematyki bloga, by zademonstrować elastyczność i uniwersalność zastosowań języka R. Przydaje się on nie tylko wtedy, gdy na świecie wybucha jakiś wulkan – pośród 18748 gotowych do użycia pakietów znajdziemy coś na każdą okazję. Wkrótce przeprowadzę szkolenie pokazujące możliwości tego języka i środowiska R Studio – zapisz się na newsletter aby nie przegapić zapisów.

PS: tak naprawdę do narysowania ilustracji wykorzystałem funkcję plot_my_connection naprawiającą usterkę poleceń gcIntermediate i lines, źródło: R Graph Gallery, autor: Yan Holtz.