Analiza danych w języku R – odcinek 10

Gdy przetwarzamy dane pomiarowe zebrane w tzw. szeregach czasowych (seria pomiarów wraz z datą wykonania), możemy potrzebować informacji na temat długoterminowej dynamiki zmian. Czasem nie będzie ona oczywista, bo np. temperatura powietrza może zmieniać się w ciągu doby o 20 stopni Celsjusza a tygodniowy trend niekoniecznie ukaże się na wykresie.

W innych sytuacjach przydatne będą obliczenia przyrostowe, np. liczba sprzedanych egzemplarzy towaru od początku roku kalendarzowego albo średnia wszystkich dotychczasowych ocen wskazanego ucznia. Jak sobie z tym poradzić?

Dziś poznamy funkcje przydatne podczas analizowania szeregów czasowych

Źródło danych

Spojrzymy na dane pogodowe z roku 2022 dla miasta Wrocławia. Zgodnie z warunkami ich użycia, zamieszczam następującą informację: Źródłem pochodzenia danych jest Instytut Meteorologii i Gospodarki Wodnej – Państwowy Instytut Badawczy. Skompresowany plik 2022_424_s.zip pobrałem z tego katalogu, pliki tamże składowane są opisane następującym schematem. Komendę wczytującą dane znajdziesz na GitHubie.

Średnia krocząca

Aby „wygładzić” dane o dużej zmienności możemy skorzystać ze średniej kroczącej, realizowanej za pomocą funkcji rollmean. Oto, w jaki sposób obliczymy dla każdego pomiaru średnią temperaturę z całej doby – ale nie doby „zegarowej”, lecz odcinka czasu rozciągającego się 12h w tył i w przód.

pogodawro %>%
mutate(srednia24 = rollmean(temp, 24, fill=NA))

Dla kilkunastu początkowych i końcowych obserwacji nie da się wyznaczyć takiej średniej, więc musimy wprost zadeklarować, że w tych wierszach wartości średniej brak (NA = brak pomiaru, wartość nieistniejąca). Parametrem align możemy przestawić tryb uśredniania z „centralnego” na „lewy” lub „prawy” (czyli uwzględnianie wybranej liczby późniejszych lub wcześniejszych obserwacji). Oprócz średniej możemy skorzystać z kroczącej mediany, sumy, czy maksimum.

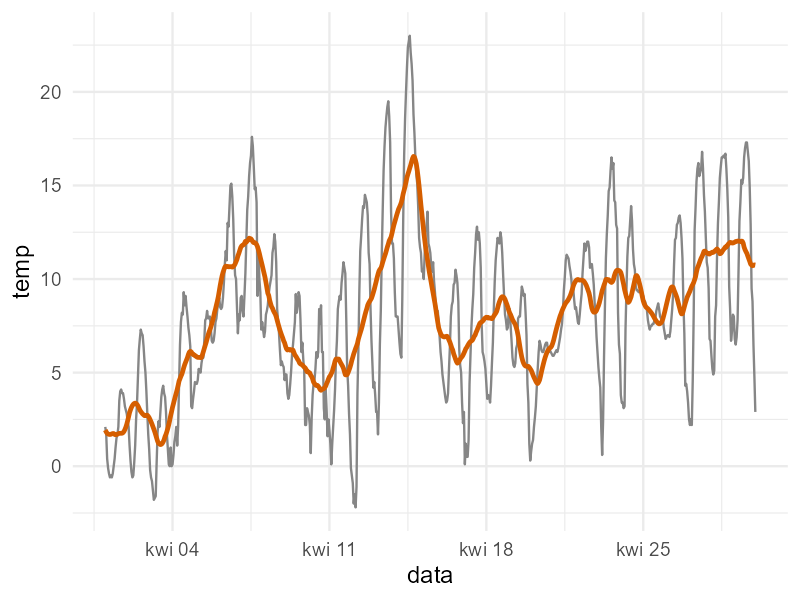
Spójrzmy na uśredniony powyższą metodą wykres temperatury z kwietnia:

pogodawro %>%
mutate(srednia24 = rollmean(temp, 24, fill=NA)) %>%
filter (data >= ymd("2022-04-01") & data <= ymd("2022-04-30") ) %>%
ggplot(aes(x=data))+
  geom_line(aes(y=temp), color="#868686")+
  geom_line(aes(y=srednia24), color="#D55E00", lwd=1)+
  theme_minimal()+
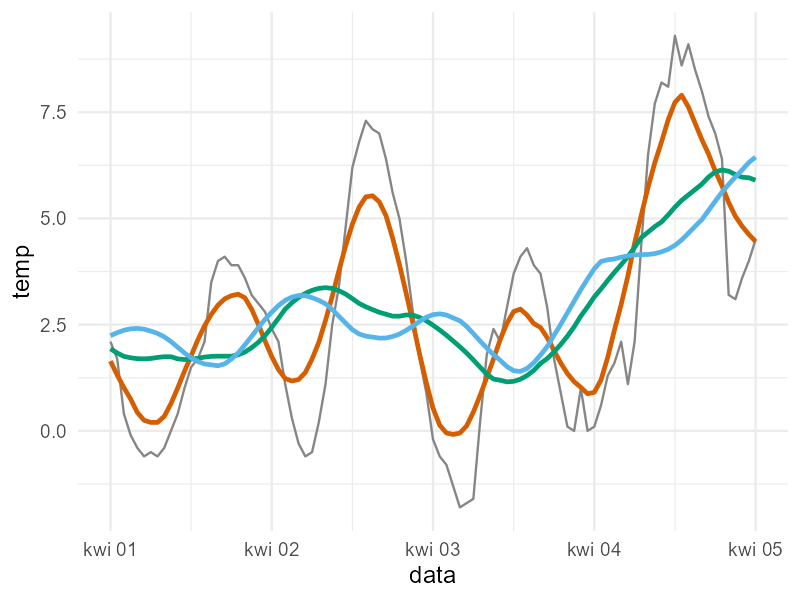
  theme(legend.position = "none")

Oto dane temperaturowe z jednego tygodnia uśrednione wg przedziałów o rozpiętości 12h (kolor pomarańczowy), 24h (zielony) i 36h (niebieski) – kod generujący wykres jest na Githubie.

Dane wcześniejsze / późniejsze

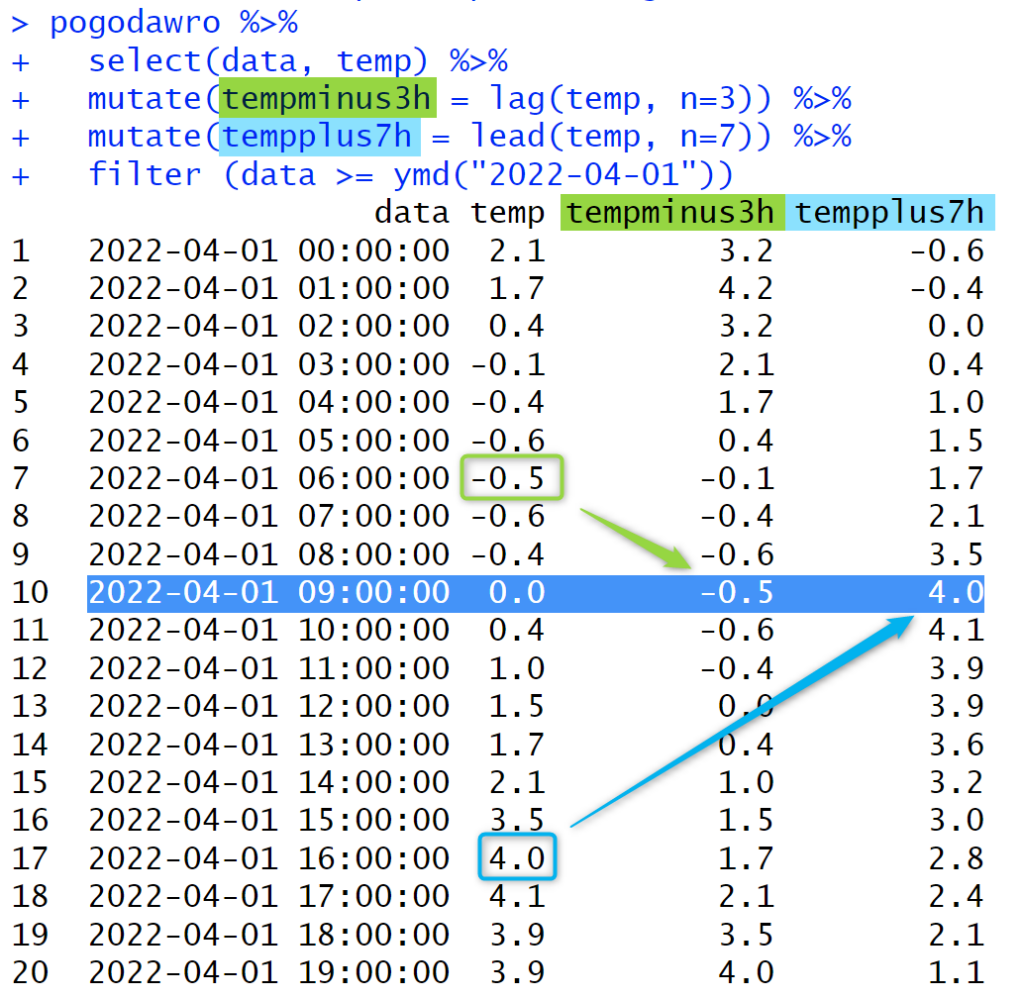
Jeśli w bieżącym wierszu potrzebujemy umieścić wartości z wierszy poprzedzających lub następujących, użyjemy funkcji lag lub lead. Na obrazku poniżej widzimy ramkę danych wzbogaconą o kolumny z pomiarem temperatury o 3h wcześniejszym i o 7h późniejszym od bieżącego. Dzięki obliczeniom tego typu można łatwo określić, czy obserwowane wartości rosną, czy też maleją.

Obliczenia skumulowane

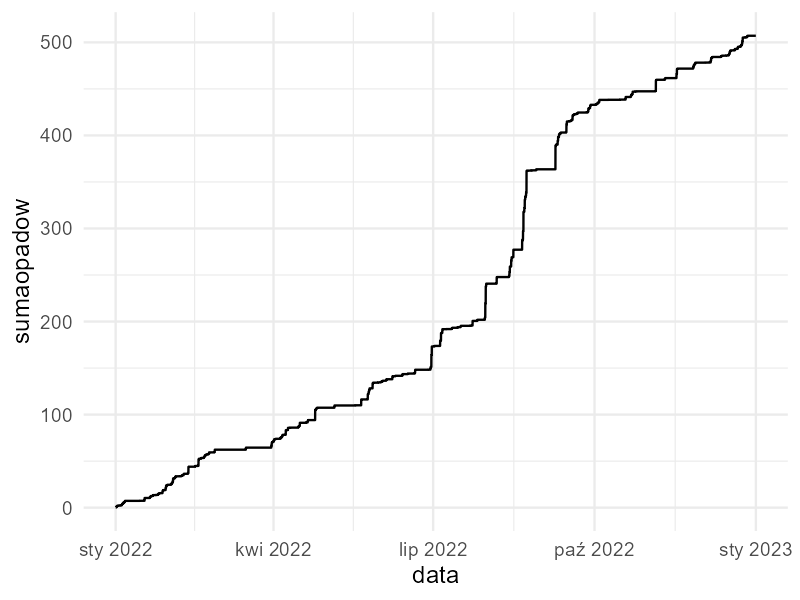
Ile wody spadło w 2022 roku we Wrocławiu? Odpowiedź obliczymy formułą sum(pogodawro$opad6h) – było to 507 mm deszczu i śniegu. Ciekawsze będzie jednak sprawdzenie, kiedy opadów było więcej, a kiedy mniej.

Funkcje kumulacyjne pozwalają wyliczyć nowe wartości w każdym wierszu na podstawie danych z wiersza bieżącego i wszystkich wcześniejszych. Uwaga – zmierzone opady pojawiają się w danych źródłowych co 6h, ale nie psuje to naszych obliczeń.

pogodawro %>%
mutate(sumaopadow = cumsum(opad6h)) %>%
ggplot(aes(x=data, y=sumaopadow))+
  geom_line()+
  theme_minimal()

Równie łatwo policzymy skumulowaną średnią (cummean) albo dotychczasowe skrajne wartości (cummin/cummax).

Rankingi

Wróćmy na chwilę do danych z Otomoto. Gdy chcemy dowiedzieć się, czy auto jest „tanie”, czy „drogie”, możemy sklasyfikować jego cenę przy użyciu funkcji ntile. Funkcja ta obliczy, do którego przedziału trafią samochody, gdy rozsortować je do wybranej liczby „kubełków” (przegródek). Przykład: jeśli określimy liczbę kubełków na cztery, dostaniemy przedziały od 1 (najtańsza ćwiartka aut w ofercie) do 4 (najdroższa ćwiartka):

otomoto$cwiartka <- ntile(otomoto$price, n=4)

Jeśli potrzebujemy większej precyzji, możemy użyć funkcji percent_rank, dzięki której dowiemy się, na jakiej pozycji plasuje się dane auto

otomoto$procent_tanszych_aut <- 100 * percent_rank(otomoto$price)

Innymi przydatnymi funkcjami szeregującymi mogą być dense_rank albo min_rank – wybór będzie zależał od bieżących potrzeb i wymogów analityka.